I. TÓM TẮT LÝ THUYẾT

1. Định nghĩa hai đường thẳng song song:
   • + Hai đường thẳng song song (trong mặt phẳng) là hai đường thẳng không có điểm chung.
2. Dấu hiệu nhận biết hai đường thẳng song song:
   • + Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng song song.
   • + Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc đồng vị bằng nhau thì hai đường thẳng song song.
   • + Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc trong cùng phía bù nhau thì hai đường thẳng song song.
   • + Ngoài ra ta còn có dấu hiệu: Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le ngoài bằng nhau thì hai đường thẳng song song.
   • Ví dụ:
   • 
   • 

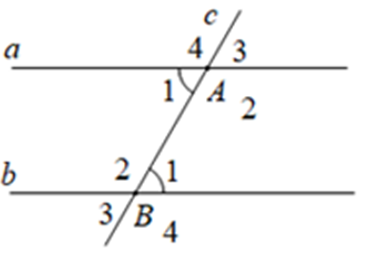
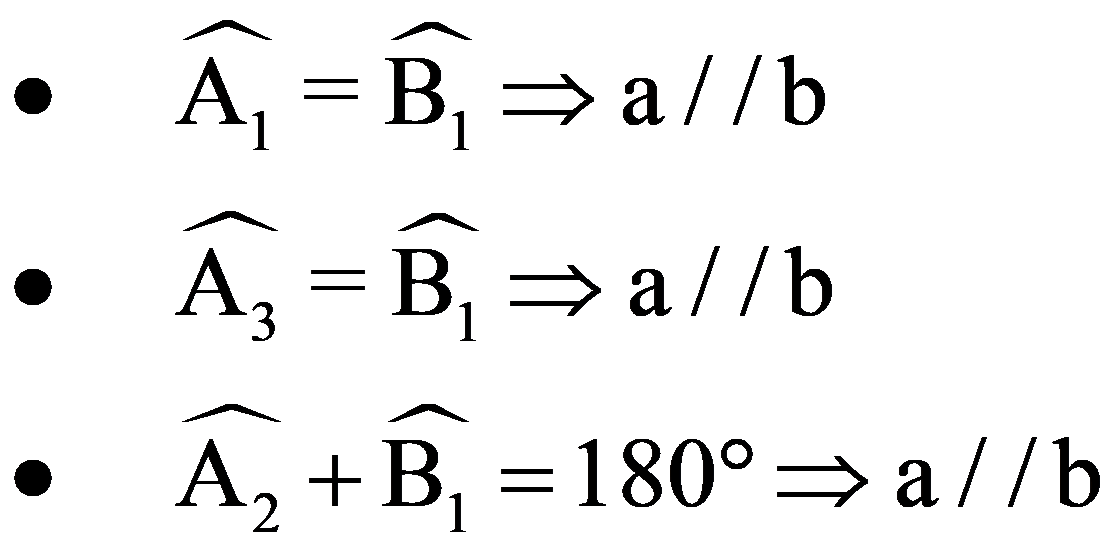
II. BÀI TẬP MINH HOẠ:

Câu 1: Cho đường thẳng a và b cắt đường thẳng c tại A và B. Cho biết tổng của hai góc trong cùng phía với một góc so le trong với một trong hai góc này bằng 300° và trong hai góc kề bù có góc này gấp đôi góc kia. Hai đường thẳng a và đường thẳng b có song song với nhau không? Vì sao?

Giải

1. a.

Câu 2: Cho hình vẽ, trong đó góc AOB = 60°, Ot là tia phân giác của góc AOB. Hỏi các tia Ax, Ot và By có song song với nhau không? Vì sao?

Câu 3: Cho góc xOy = 30° và điểm A nằm trên cạnh Ox. Dựng tia Az song song với tia Oy và nằm trong góc xOy.

1. Tìm số đo góc OAz?
2. Gọi Ou và Av theo thứ tự là các tia phân giác của góc xOy và xAz. Chứng tỏ rằng Ou song song với Av.

Câu 4: Cho góc xOy = α, điểm A nằm trên tia Oy. Qua A vẽ tia Am. Tính số đo góc OAm để Am song song với Ox.